1936. Авиаперелёты

Главного конструктора Петю попросили разработать новую модель самолета для компании “Air Бубундия”. Оказалось, что самая сложная часть заключается в подборе оптимального размера топливного бака.

Главный картограф “Air Бубундия” Вася составил подробную карту Бубундии. На этой карте он отметил расход топлива для перелета между каждой парой городов.

Петя хочет сделать размер бака минимально возможным, для которого самолет сможет долететь от любого города в любой другой (возможно, с дозаправками в городах на пути следования).

Вход. Первая строка содержит количество городов в Бубундии n (1 ≤ n ≤ 1000). Далее идут n строк по n чисел каждая. j-ое число в i-ой строке равно расходу топлива при перелете из i-ого города в j-ый. Все числа не меньше нуля и меньше 10⁹. Гарантируется, что для любого i в i-ой строке i-ое число равно нулю.

Выход. Одно число – оптимальный размер бака.

Пример входа	Пример выхода
4 0 10 12 16 11 0 8 9 10 13 0 22 13 10 17 0	10

РЕШЕНИЕ

графы – сильная связность

Анализ алгоритма

Пусть размер бака равен x. Построим граф, в котором существует ориентированное ребро (i, j) тогда и только тогда, когда объем топлива, необходимый для прямого перелета из i-го города в j-ый не больше x (то есть с имеющимся баком можно совершить прямой перелет).

Из любого города можно перелететь в любой, только если граф является сильно связным. Вместо вычисления количества сильно связных компонент воспользуемся следующим свойством.

Граф является сильно связным, если для любой вершины v имеют место следующие утверждения:

· из вершины v существует путь во все остальные вершины;

· из любой вершины существует путь в v;

Причем если эти утверждения выполняются хотя бы для одной вершины v, то они выполняются и для всех остальных вершин. Проверку этих свойств можно реализовать, запустив поиск в глубину на графе, например из нулевой вершины (пусть для определенности вершины нумеруются числами от 0 до n – 1).

Таким образом для бака размером x мы научились определять, сможет ли добраться самолет из любого города в любой другой. Остается найти искомый минимально возможный объем бака самолета методом бинарного поиска.

Пример

Граф, заданный в примере, имеет вид:

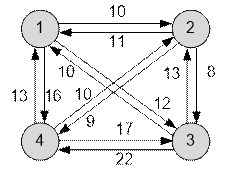
С левой стороны приведем граф возможных перелетов с объемом бака равным 9, а справа с объемом 10.

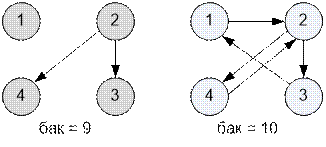
При величине бака 10 самолет сможет долететь от любого города в любой другой.

Реализация алгоритма

Матрицу расхода топлива между городами храним в массиве graph. Массив used используется для отмечания уже пройденных вершин.

#define MAX 1010

int graph[MAX][MAX], g[MAX][MAX];

int used[MAX];

Запускаем процедуру поиска в глубину dfs из вершины v. Если type = 0, то идем по ребрам согласно их направлению. При type = 1 поиск в глубину совершаем по ребрам в обратном направлении.

void dfs(int v, int type)

{

used[v] = 1;

for(int i = 0; i < n; i++)

if ((type ? g[i][v] : g[v][i]) && !used[i]) dfs(i,type);

}

Функция AllVisited проверяет, были ли посещены все ребра графа при обходе в глубину. Ответ будет положительный и функция возвратит 1, если все ячейки массива used содержат единицу.

int AllVisited(void)

{

for(int i = 0; i < n; i++)

if (!used[i]) return 0;

return 1;

}

Основная часть программы. Читаем входную матрицу расхода топлива в массив graph.

scanf("%d",&n);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

scanf("%d",&graph[i][j]);

Минимальный размер бака ищем бинарным поиском на отрезке [L; R]. Изначально положим [L; R] = [0; 2000000000].

L = 0; R = 2000000000;

while(L < R)

{

Mid = (L + R) / 2;

На каждой итерации бинарного поиска строим матрицу смежности g ориентированного графа: g[i][ j] = 1, если из города i в город j можно совершить прямой перелет с объемом бака Mid.

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

g[i][j] = (graph[i][j] <= Mid);

Запускаем поиск в глубину из нулевой вершины. Если из нулевой вершины можно достичь все остальные, а изо всех остальных вершин – нулевую, то граф сильно связный. В таком случае значение переменной flag остается равным 0.

memset(used,0,sizeof(used));

dfs(0,0); flag = 0;

if (AllVisited())

{

memset(used,0,sizeof(used));

dfs(0,1);

if (!AllVisited()) flag = 1;

} else flag = 1;

В зависимости от значения flag пересчитываем границы интервала бинарного поиска.

if (!flag) R = Mid; else L = Mid + 1;

}

Выводим искомый минимальный размер бака L.

printf("%d\n",L);

Java реализация

import java.util.*;

public class Main

{

static int graph[][];

static boolean g[][], used[];

static int n;

//type = 0 original edges

//type = 1 reversed edges

static void dfs(int v, int type)

{

used[v] = true;

for(int i = 0; i < n; i++)

if ((type == 1 ? g[i][v] : g[v][i]) && !used[i]) dfs(i,type);

}

static boolean AllVisited()

{

for(int i = 0; i < n; i++)

if (!used[i]) return false;

return true;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

graph = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

graph[i][j] = con.nextInt();

g = new boolean[n][n];

used = new boolean[n];

int L = 0, R = Integer.MAX_VALUE;

while(L < R)

{

int Mid = (L + R) / 2;

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

g[i][j] = (graph[i][j] <= Mid);

Arrays.fill(used, false);

dfs(0,0);

boolean flag = false;

if (AllVisited())

{

Arrays.fill(used, false);

dfs(0,1);

if (!AllVisited()) flag = true;

} else flag = true;

if (flag == false) R = Mid; else L = Mid + 1;

}

System.out.println(L);

con.close();

}

}